Consommation d'air en plongée avec bouteille

Introduction

Si vous avez regardé l'émission "C'est pas sorcier" consacrée à la plongée, on y apprend que les poumons de Frédéric ne sont pas des compresseurs. Il a rapidement atteint une profondeur limite avec son tuba de 4 mètres. Il lui faut s'équiper de bouteilles pour avoir de l'air à la pression locale et continuer à descendre.

La consommation d'air est dépendante de la profondeur. En s'affranchissant de toutes les considérations physico-chimiques (température, variation des volumes...) et physiologiques (narcose, hyperoxie, essoufflement, paliers, résistance du corps...), cet article expose le calcul pour trouver la majoration de la profondeur humainement atteignable avec des bouteilles.

Le schéma suivi est simple : le plongeur s'immerge à vitesse constante et remonte à mi-bouteille. Le calcul commence donc par établir la formule donnant la consommation d'air durant la descente.

Éléments du calcul

Déterminons tout d'abord les caractéristiques connues que sont la vitesse de descente, la consommation d'air instantanée, la profondeur maximale règlementaire (ici un niveau 2), le volume de la bouteille et sa pression initiale. Il s'agit donc d'un cas classique simple.

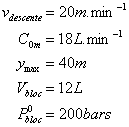
Supposant être au niveau de la mer, posons les relations entre la pression (bar), la profondeur (m) et le temps maximal de descente (min) :

Consommation d'air durant la descente

Dans la phase de descente, le calcul suivant est parfaitement compatible avec la réalité.

La consommation recherchée est la somme infinie de la consommation instantanée à chaque profondeur durant tout le temps de descente.

La formule est logique :

• Si on consomme beaucoup en moyenne (C_0m), la consommation finale augmente.
• Si on descend vite (v_descente), la consommation diminue puisqu’il faudra moins de temps pour rejoindre la profondeur maximale.
• Si on va plus profond (y_max), la consommation augmente puisqu’il faut plus de temps pour rejoindre la profondeur maximale.

Le profil de consommation d'air à la descente est polynomial :

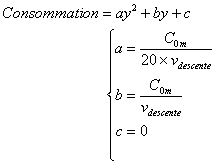
Appliquons la formule avec nos chiffres du début :

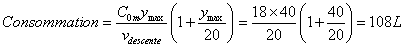
Pour une bouteille de 15 L gonflée à 200 bars, cela correspond à 3,6% de la capacité. Pour une bouteille de 12 L gonflée à 200 bars, cela correspond à 4,5% de la capacité. En prenant une marge de 50 bars de réserve (c'est-à-dire qu'on retire dans lee calcul 50 bars à la pression de la bouteille), la part s’élève respectivement à 4,8% et 6% pour une descente à 40 mètres.

Consommation d'air durant la remontée

Du fait de la diffusion du diazote dans le sang durant le temps de descente et de plongée, la remontée ne peut pas s'effectuer dans les mêmes conditions. La remontée avec les paliers et la vitesse différente qu'à la descente rend impossible notre exercice de calcul mathématique.

Bien que ce soit faux, on supposera que la remontée se fait comme la descente en sens inverse, avec une ignorance égale à celle d'une humanité qui n'aurait jamais plongé de tout temps.

La profondeur maximale atteignable est alors donnée à mi-bouteille. Le trajet de la plongée est alors un triangle isocèle. En consommant intégralement la réserve, le plongeur finit la dernière inspiration de la bouteille au moment où il refait surface. Dans la vraie vie, il est certain que vous ne feriez pas çà...

Avec toutes ces hypothèses capillotractées, on va savoir rapidement à partir de quelle profondeur les poissons ne seront jamais dérangés par un homme-grenouille.

Profondeur maximale atteignable

Pour la trouver, il suffit de résoudre une équation où y_max est l'inconnue :

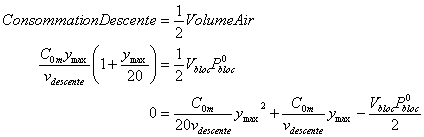
Il s'agit d'une équation polynomiale de degré 2. Le polynôme a les coefficients et racines suivantes :

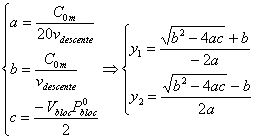
La logique physique ne permet qu'une seule profondeur possible et le premier résultat est manifestement négatif. Le second résultat est possible si :

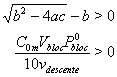
En explicitant, la descente n'est pas possible si :

• On est en apnée (C_0m=0).
• On oublie sa bouteille (V_bloc=0).
• La bouteille est vide (P⁰_bloc=0).
• On refuse de couler (v_descente=0).

Ces conditions très évidentes étant remplies, nous pouvons simplifier le résultat :

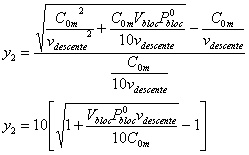
La formule est cohérente :

• L'augmentation du volume de la bouteille, de sa pression ou de la vitesse de descente permet d'aller plus profondément.
• Si la consommation d'air augmente, la profondeur atteignable est plus faible.

En appliquant les valeurs numériques, nous obtenons :

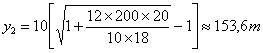
Pour une telle profondeur, le temps de descente serait de :

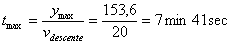
Le temps total de plongée est le double.

Limitations

Comme déjà indiqué, les résultats incluant la remontée n'ont aucune réalité physique mais permettent d'estimer facilement une majoration de la limite maximale humainement atteignable avec des bouteilles classiques.

En réalité, il existe des limites restreignant cette profondeur à beaucoup moins que ça :

• La narcose (dite "mal des profondeurs") apparaît vers 35 m. C'est une perturbation grave du système nerveux par le diazote.
• Le dioxygène devient toxique à 66 m, car si on multiplie la pression locale de 7,6 bars par le taux normal de dioxygène dans l'air comprimé (21%), on obtient une pression partielle de 1,6 bars qui est considérée comme la limite avant l'hyperoxie. C'est l'effet Paul Bert.
  • Il existe aussi l'effet Lorrain Smith qui dit qu'une exposition de plus de 2 heures à 0,5 PpO₂ est nuisible pour les poumons. Cette pression partielle correspond à 14 mètres de fond.
• Un manque de respiration peut provoquer un mal de crâne aigu à cause du dioxyde de carbone qui s'accumule dans le cerveau.
• Des paliers doivent être effectués à la remontée suite à la diffusion dans le corps du diazote au moment de la descente et de la plongée elle-même.
• La remontée est toujours plus lente que la descente.

Voilà pour les aspects mathématiques. Et ça n'empêche pas des plongeurs hyperbares de descendre à 701 mètres de profondeur pour réaliser des travaux de maintenance pétrolière (voir "C'est pas sorcier").

Dernière modification le 3 février 2017 à 01:06