Jeu de la fête foraine pour gagner des produits Apple : recouvrez le cercle

Dans les fêtes foraines, fini la peluche made in China partout, on peut maintenant gagner des produits technologiques, dont Apple est l'égérie. Pensez-vous vraiment pouvoir gagner facilement ? Démonstration.

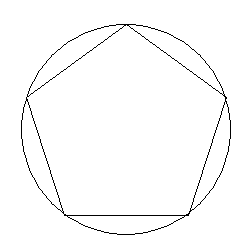
Je souhaite considérer l'un de ces jeux qui consiste à masquer un disque avec d'autres disques. Il existe deux variantes : lancer 3 disques de loin pour recouvrir un disque associé à un cadeau, ou recouvrir à la main un disque avec 5 autres. Intéressons nous à ce dernier de façon mathématique, et posons-nous la question : quelle est l'astuce du jeu et quelle est celle du forain pour s'en prémunir ? De là découleront la condition de victoire et la stratégie pour savoir si on a perdu avant même d'avoir fini.

L'idée première est positionner les 5 cercles sur un pentagone inscrit dans le cercle à recouvrir.

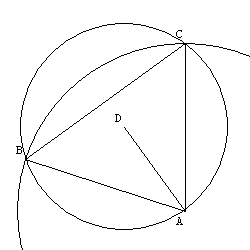
Le pentagone est une forme régulière : les arêtes ont la même longueur, les angles appuyés sur les arêtes sont tous les mêmes, et les sommets sont à la même distance du centre. Dans ce cas de figure, utilisons la propriété de l'inscription du cercle dans un triangle isocèle. Nous obtenons cette figure :

Le segment [BC] est une arête du pentagone. Le segment [AD] est le rayon des 5 petits disques à placer. Le triangle ABC est seulement isocèle, car l'angle BÂC fait 72° et non 60° (ce serait le cas en présence de 6 disques à placer). Le cercle de centre D passe par les points A, B et C, il est donc circonscrit au triangle ABC.

Dans cette hypothèse, le positionnement du premier disque conditionne la victoire. Il doit être placé tel que présenté sur la figure précédente. Le deuxième disque est positionné pour passer par les points A et C (condition suffisante). Et ainsi de suite jusqu'à recoller tous les morceaux.

La chance du forain est de pouvoir agir sur deux faits implacables.

• Le premier fait est géométrique: le forain fournit le matériel. C'est lui qui détermine les proportions entre le disque à recouvrir et les disques-satellites. Le ratio des dimensions donne la marge d'erreur. Plus celle-ci est faible, moins vous avez de chances de gagner et mieux le forain peut gagner sa journée.
• Le deuxième fait est humain: il faut trouver le centre du disque central au micromètre près. Généralement possible avec une règle et un compas, vous n'aurez en pratique que vos yeux pour juger et pleurer ! Si vous arrivez à placer le premier disque et trouver le centre, vous êtes en mesure de finir le puzzle.

Mais alors, quelle est la condition mathématique de réussite ? Nommons "R" le rayon du grand disque (AC sur la figure) et "r" le petit rayon (AD sur la figure). Comme AD=DC par propriété du cercle, le triangle ADC est isocèle et nous avons donc la relation suivante par projection et trigonométrie :

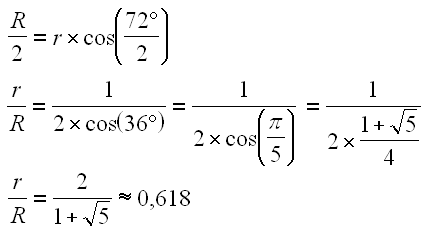
Cela veut dire que le forain ne peut pas vous proposer des disques dont le ratio des diamètres serait inférieur à 61,8%. En pratique, ce sera le cas, et c'est là qu'il faut peut-être moins se risquer. Voyez pourquoi.

Dans le jeu en ligne suivant, le grand disque a un diamètre de 297 pixels et le petit de 181 pixels, soit un ratio de 61% (hum ?). J'ai suivi au pixel près de mon écran la démonstration de cet article, et après une quinzaine de tentatives qui m'ont virtuellement coûté 150€ (10€ étant le prix réel d'une partie !), je n'ai pas fait mieux que 6 pixels non recouverts. L'échec est à mettre sur le compte des mathématiques, car il existe une meilleure solution que celle précédemment expliquée. C'est en effet l'occasion de remarquer que certains disques ne passent pas par le centre. Pourquoi ?

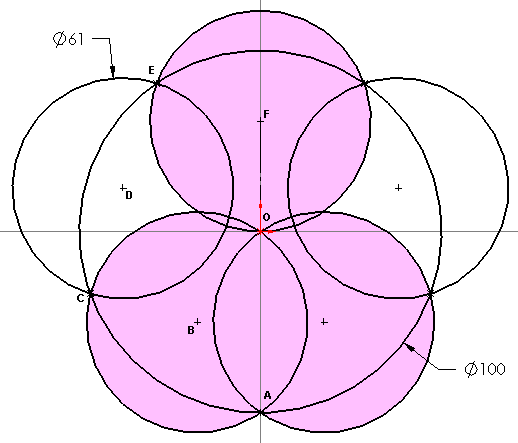
Quand on superpose des cercles les uns par rapport aux autres, des zones communes se dessinent. Dans notre situation, les cercles roses couvrent des zones que les deux cercles blancs n'ont plus à recouvrir. Si l'on prend en compte ce facteur, deux des disques ne passent plus par le centre :

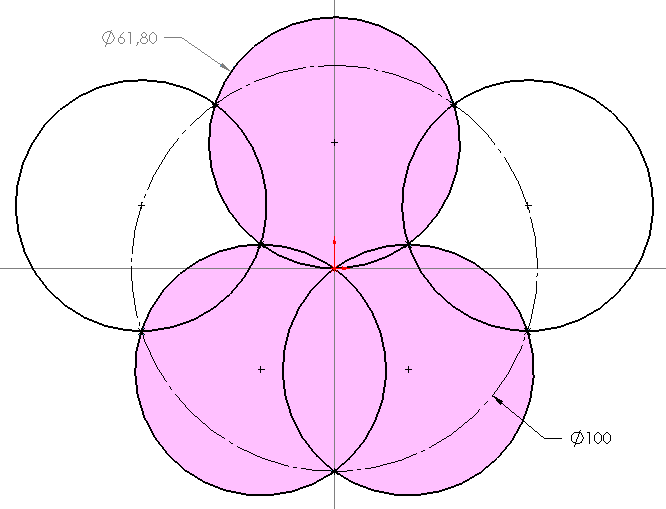
Sur la figure ci-dessus construite avec un logiciel de CAO paramétrique (vous donnez les contraintes, il donne la forme), on constate que la côte pilotée affiche également 61,8%. Il y a encore trop de contraintes. On peut donc faire sauter les deux contraintes d'intersection des cercles blancs avec les zones roses au centre, et ainsi s'apercevoir que l'on peut réduire les dimensions par simulation jusque 60,996% (côte pilotante).

On va analyser plus en détail la relation mathématique de cette figure compliquée. On reprend la notation de la figure précédente, et nous obtenons ce nouveau schéma avec quelques chiffres pour vous convaincre des formules. Pour rappel, les calculs qui suivent sont exprimés en radians et non pas en degrés.

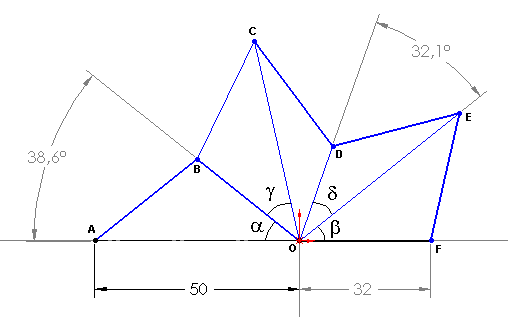
A l'aide de considérations géométriques sur les angles, les triangles isocèles et les bissectrices, on tire les relations suivantes :

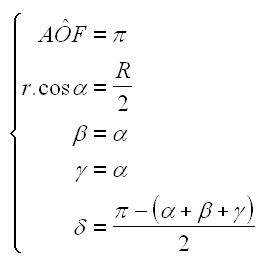
En fusionnant toutes ces relations, on trouve aisément la valeur de delta :

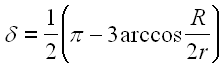
Cette relation n'est pas suffisante pour trouver la solution, car il reste deux inconnues : "r" et "delta". Si on revoit plus haut la figure globale, on peut émettre comme postulat (il me manque la justification) que --les points C, D et E sont alignés--. Sous cette condition, on fait apparaître un triangle rectangle qui permet de relier les inconnues comme suit :

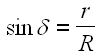
En regroupant une fois de plus nos relations, on découvre la condition mathématique générale utilisée par notre forain pour vous donner le moins de chance possible de gagner. Je pose p=r/R comme le ratio des rayons, car le problème est indépendant de la taille des disques.

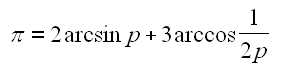
Il n'est pas possible d'isoler la valeur de "p" de façon formelle, car les fonctions arccos et arcsin ne peuvent pas être exprimées de façon simple. Cependant, avec une recherche dichotomique, on peut trouver une solution approchée. Il s'agit de 60,99579% ! Le résultat est conforme à celui obtenu précédemment par simulation graphique. Le code Maple suivant permet de faire une recherche dichotomique sur la fonction qui est strictement croissante sur le domaine de définition ]0,5..1,0[ :

#-- Définitions
f:=x->evalf(2*arcsin(x)+3*arccos(1/(2*x))-Pi):
vmin := 0.5:
vmax := 1.0:

#-- Boucle dichotomique
for k from 1 to 100
do
val := (vmin+vmax)/2:
if (f(val) < 0) then
vmin := val:
else
vmax := val:
fi;
end;

#-- Résultat
evalf(vmin);
evalf(vmax);

En tout cas, le jeu en ligne joue avec le feu avec son 61% vu la très faible marge de manoeuvre...

En conclusion, pour vérifier l'honnêteté du forain, ses disques doivent avoir un ratio compris entre 60,996% et 61,8%. En dessous de 61, c'est un charlot. Au dessus de 61.8, c'est un chic type. Mais existe-t-il ?

Maintenant que vous avez tout compris, analysez donc cette vidéo YouTube pour révéler la raison de sa facilité.

Posté par admin le 9 juin 2012 à 15:30 - Sciences
Texte soumis à la licence du site, sauf mention contraire
Rechercher plus d'informations

Commentaires

Evaluer l'article :

Ajouter un commentaire