Toujours le chemin le plus court

Au lycée, les élèves étudient le phénomène de la diffraction via la loi de Snell-Descartes qui nous dit que : n₁.sin(i₁) = n₂.sin(i₂).

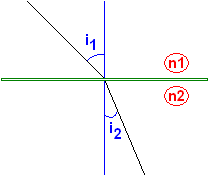
Tous les phénomènes optiques que nous rencontrons dans la vie courante (réfraction, miroir...) s'expliquent en fait par ce qu'on appelle le Principe de Fermat. Celui-ci non démontré (c'est un principe) nous dit que la lumière relie deux points en un temps minimal. La conséquence immédiate est que la lumière se propage rectilignement.

La loi de Snell-Descartes est déduite du principe de Fermat. En effet, c'est la seule condition qui permette de trouver une solution à ce problème : quel est le chemin le plus rapide pour lier A et C ?

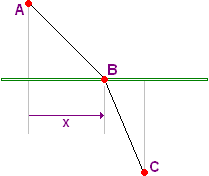
Avec les coordonnées des points A et C, on déduit le temps nécessaire pour parcourir la longueur AB+BC. Ca fait apparaître les indices de réfraction (rapport de la vitesse de la lumière dans le vide sur celle dans le milieu considéré). Ensuite la dérivation par rapport à x puis la recherche du minimum font apparaître la formule de Snell-Descartes. Cette démonstration est très fastidieuse, mais il en existe des plus simples avec des vecteurs.

Ça n'a l'air de rien, mais tout ce charabia explique que dans les compétitions de natation, il n'est pas utile de plonger le plus loin possible pour être le premier. Non non, il suffit de plonger au bon endroit pour prendre le chemin le plus rapide... Dans cet exemple, vous êtes la lumière et vous allez moins vite sous l'eau que sur terre.

Posté par admin le 30 octobre 2008 à 18:07 - Sciences
Texte soumis à la licence du site, sauf mention contraire
Rechercher plus d'informations

Commentaires

Evaluer l'article :

Ajouter un commentaire