La notation des QCM et espérance

La hantise des lycéens est le QCM ! Il s'agit du seul examen où l'on peut perdre des points lorsqu'on ne sait pas répondre. Que tout le monde se rassure : si vous aviez des mauvaises notes à l'école, il se peut que vous n'y soyez pour rien. Les QCM sont parfois involontairement prévus pour vous faire perdre.

Exemple : 4 propositions de réponse, 1 point par bonne réponse, 0 point pour une non-réponse, et -0.5 point par mauvaise réponse.

Le point de sanction est calculable. Dans l'exemple ci-dessus, il est exagéré et nous allons le démontrer.

L'hypothèse de base d'un QCM doit être : "si je ne sais pas et que je réponds au pif, je dois avoir zéro". Par conséquent, l'espérance mathématique à la question doit être nulle.

Soit :

• q la probabilité de choisir au pif la bonne réponse
• G le point qu'on peut gagner
• P le point qu'on peut perdre
• N le nombre de propositions
• E l'espérance à la question

Dans la mesure où l'absence de réponse ne coûte aucun point, la proposition "Je ne sais pas" doit être éliminée du calcul. Ce n'est pas une réponse au pif.

En supposant qu'il n'y a qu'une seule bonne réponse par question, nous avons donc :

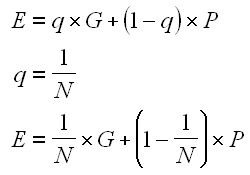
D'où nous tirons les formules magiques :

Pour l'exemple donné en début d'article, si on applique la première formule, on déduit qu'on peut gagner en répondant au pif : (1+(4-1)*-0.5)/4 = -0.125 point. Le diable !

Par contre, si on ne donne que 3 propositions, le calcul est tout à fait équilibré. Pour augmenter ses chances, le candidat peut faire des éliminations. Ainsi, en retirant la plus idiote, il reste 2 propositions et il peut espérer gagner 0,25 pt.

De manière générale, comment mettre en place un barême ? Tout simplement à l'aide de la seconde formule exprimant P. Sachant qu'on souhaite une espérance nulle (E=0) et qu'on donne généralement 1 point par question (G=1), nous avons :

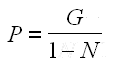
Dans notre exemple : N=4 et G=1. Moralité, la sanction idéale n'est pas -0,5 mais 1/(1-4) = -0,33.

Maintenant que vous avez tout compris, venons-en à la télévision.

Inutile de préciser qu'ils ne peuvent pas se tromper... et que ce n'est pas la question à 1 million d'euro !

Pour terminer sur un cas de figure particulier : lorsque plusieurs réponses sont possibles et qu'il faut les sélectionner toutes pour avoir le point, il faut considérer les combinaisons mathématiques. S'il y a 2 réponses parmi 4, on n'a pas 2 chances sur 4 mais 1 chance sur 6 de réussir. Il ne faut donc jamais se hasarder sur de telles questions, parce que l'espérance est très proche du point sanction.

Voilà, vous savez (presque) tout.

Posté par admin le 15 avril 2010 à 21:53 - Sciences
Texte soumis à la licence du site, sauf mention contraire
Rechercher plus d'informations

Commentaires

Evaluer l'article :

Ajouter un commentaire