
Pourquoi le V-Cube 7 est-il rond ?
Pour rappel là et là, le terme "V-Cube" désigne des casse-têtes "cube" de dimension 5 à 7. Ils sont les directs concurrents des cubes de Rubik, mais sont d'une qualité, technologie et finesse nettement plus supérieurs.
Mais puisqu'on parle de casse-tête "cube", pourquoi le V-Cube 7 est-il rond ? Les V-Cube 5 et V-Cube 6 sont cubiques pourtant. De la même façon, pourquoi les V-Cube 8, V-Cube 9, V-Cube 10 et V-Cube 11 sont-ils eux-aussi ronds sur le papier ?
L'explication est simplement mathématique. En effet, le gros cube est divisé en sous-cubes. Ceux-ci tournent autour d'un centre auquel ils sont rattachés mécaniquement. En effet, s'ils étaient flottants, on pourrait les enlever et le cube n'aurait plus aucune consistance.
Quand une couronne est orientée de 45°, le cube du coin se présente ainsi (dimension 5) :
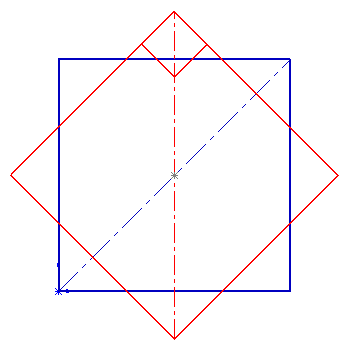
Entre l'arête horizontale du grand cube et le coin inférieur du petit cube, on a une distance en projetant orthogonalement. Son signe nous donne la condition nécessaire pour que le cube soit ou non rond. En fonction des contraintes physiques, elle pourra être suffisante aussi.
En dessinant le cube de dimension 7, on constate que le cube extérieur serait éjecté s'il n'était pas tenu. En arrondissant les arêtes du gros cube (trait vert), on compense la limitation physique.
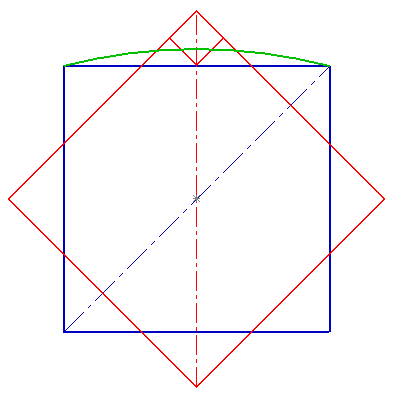
On devine aisément que plus la dimension est grande, plus le cube doit être excurvé.
On peut ajouter que le phénomène que nous expliquons est bien sûr indépendant (mathématiquement) de la taille du cube.
A l'aide des schémas précédents, pour que le cube soit cubique, nous déduisons qu'il faille que "la demi-diagonale du grand cube soustrait de la diagonale du petit cube extérieur doit être strictement inférieure à la moitié de la longueur de l'arête du grand cube". Soit N la dimension limite du cube, nous l'isolons :

En travaillant sur des dimensions entières, nous confirmons bien notre constatation initiale : tout cube de dimension 7 et plus est nécessairement arrondi.
Notons au passage qu'il existe un V-Cube 6 arrondi, dit "B". L'explication est essentiellement mécanique. Celui cubique (dit "A", en vente) présente des arêtes plus larges que les centres pour compenser les problèmes non mathématiques.
 admin le 22 avril 2010 à 22:49 - Sciences
admin le 22 avril 2010 à 22:49 - Sciences
Texte soumis à la licence du site, sauf mention contraire
Rechercher plus d'informations




