A la découverte du rhombododécaèdre

Derrière ce nom barbare se cache un solide géométrique aux fortes propriétés. Il y a assez peu d'informations le concernant, c'est pourquoi nous allons présenter ici certaines de ses caractéristiques.

Ce solide est formé de 12 losanges agencé de la façon suivante :

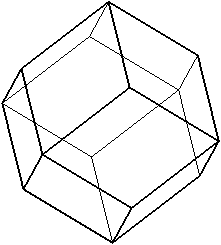
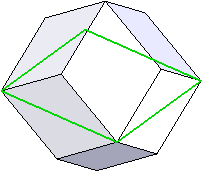
En reliant les petites diagonales des losanges, on dessine un cube lorsque le rhombododécaèdre est régulier (voir condition plus bas) ou un pavé lorsqu'il n'est pas régulier.

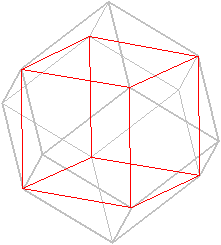
Une autre façon de révéler le cube est d'entailler le solide :

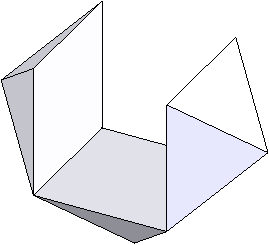
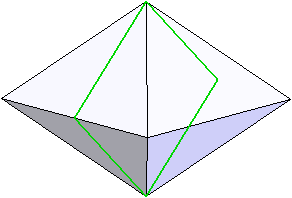
Le solide présente de nombreuses particularités physiques. En supposant qu'il soit régulier (donc il s'appuie sur un cube), on identifie des formes par projection : des carrés et des hexagones. Ces projections nous indiquent qu'il y a 3 manières de construire le solide.

Méthode n°1 : addition. On dessine un premier cube, on fait un lissage pour sortir un sommet. Par un jeu de symétries axiales, on répète les extrusions "externes". Cette technique n'est pas très viable, car on a des équations et des calculs flottants dans tous les sens. De plus, le rendu final laisse entrevoir des traits inesthétiques.

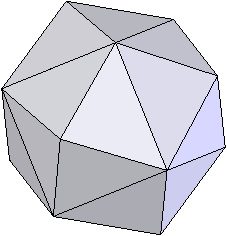
Méthode n°2 : soustraction à partir d'hexagones. On extrude un hexagone et on enlève le même selon un axe perpendiculaire. Ensuite, on ôte des coins pour faire apparaître des losanges. Avec 3 symétries selon un plan, on obtient les dernières formes. Le résultat est plutôt bon, mais on peut faire plus simple.

Méthode n°3 : soustraction à partir de carrés. En trois opérations, c'est plié ! Pour se conformer à toutes les situations possibles, on soustraira avec des losanges plutôt.

Construire le rhombododécaèdre

Il faut se donner une notation. a est la grande diagonale du losange, b est la petite diagonale. Le solide final est dit régulier si on a la relation suivante, conséquence immédiate du théorème de Pythagore :

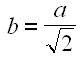
1) Première étape : extruder un losange en plan milieu sur la distance *2b. Notez que la distance b** se prend entre les milieux de deux côtés du losange. Il ne faut pas être surpris de la position de côtes, elles se verront correctement à l'étape n°3.

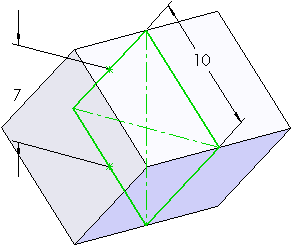
2) Deuxième étape : en prenant le plan orthogonal, enlevez la matière extérieure au cube s'appuyant sur les milieux d'arêtes. Aucune côte n'est nécessaire puisque vous avez extrudé sur la bonne longueur.

3) Enfin, en prenant le solide par le dessus, vous enlevez encore la matière à l'extérieur du troisième carré qui saute à vos yeux.

Actuellement, votre solide n'est pas régulier. Ayant a=10 et b=7, la condition n'est pas vérifiée. En ajoutant 3 équations à votre construction, vous obtenez le vrai solide.

Pavage

Avec de telles caractéristiques, le rhombododécaèdre peut paver l'espace. Quelles que soient les valeurs de a et de b, vous pouvez empiler le solide dans l'espace sans laisser le moindre espace vide.

En pavant virtuellement, on confirme la remarque. C'est beaucoup plus rapide que de faire un test grandeur nature.

Chimie

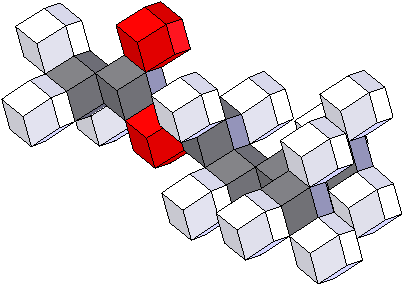
Grâce au rhombododécaèdre, on peut mettre Cram et Lewis au placard. Avec des couleurs et un peu d'initiative personnelle, on peut représenter des molécules dans l'espace.

Voici l'acide éthanoïque : CH3-COOH.

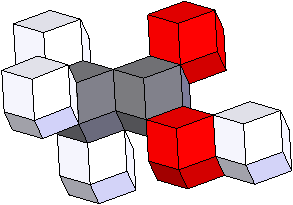
Avec plus de douceur, voici aussi l'acétate de 3-méthylbutyle : CH3-C00-CH2-CH2-CH-(CH3)2. Communément, c'est l'odeur de banane.

Posté par admin le 17 juin 2010 à 20:36 - Sciences
Texte soumis à la licence du site, sauf mention contraire
Rechercher plus d'informations

Commentaires

Evaluer l'article :

Ajouter un commentaire