Plusieurs façons d'écrire le chiffre 1
A l'aide d'un raisonnement mathématique, on peut montrer aisément qu'il existe 3 écritures équivalentes du chiffre 1, dont une seule (seulement) peut être couchée sur le papier.
La solidité du raisonnement n'est pas garantie mais le résultat est troublant.
0,999... = 1
Un zéro suivi d'une virgule et d'une infinité de 9 équivaut à 1.
0,999... ne peut pas être écrit sur le papier. En effet, si on arrête d'écrire les 9, il suffit de rajouter encore un 9 pour obtenir un chiffre encore plus près de 1, témoignant ainsi que le chiffre tronqué ne peut pas être égal à 1.
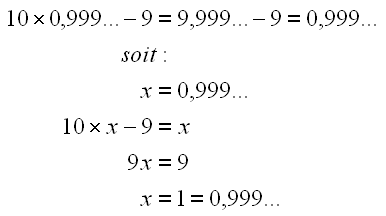
1,000...1 = 1
On peut montrer de la même façon que 1,000...1 équivaut à 1 puisque c'est le symétrique de 0,999... par rapport à 1.
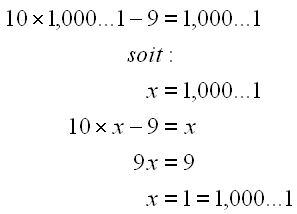
Ces résultats ne sont pas transposables aux nombres irrationnels. Ils ont une écriture unique puisque leurs décimales ne se répètent pas périodiquement (hypothèse des démonstrations précédentes). Pi, Racine de 2 ou Exponentielle de 1 sont des exemples caractéristiques.
admin le 20 mai 2010 à 22:23 - Sciences
Texte soumis à la licence du site, sauf mention contraire
Rechercher plus d'informations
Commentaires
Ajouter un commentaire
