Pourquoi le V-Cube 12 n'existera pas ?

Avant de poursuivre cet article, il est bon de relire la présentation préliminaire qui détaille les raisons de certaines hypothèses.

On a donc découvert qu'il faut d'autant plus courber les faces extérieurs du cube que la dimension augmente. En faisant des considérations purement géométriques, on devine que la courbe limite ne peut être que la sphère.

En tirant les centres des faces et en réduisant les coins, le N infini ressemble à l'image suivante (proportions non conservées) :

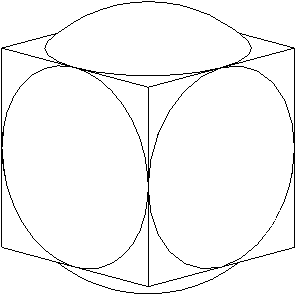
Pour conserver un pseudo-cube sans tomber dans le domaine de la sphère, il est physiquement préférable de tolérer un certain pourcentage de dépassement par rapport à l'arête du grand cube. Notons le R et reprenons le calcul du précédent article :

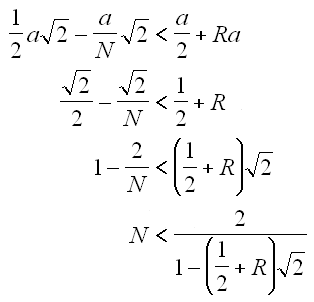
Reste à déterminer la valeur de R qui est nécessairement positive. On sait déjà que le dépassement maximal (en valeur) sera le rayon de la sphère maximale soustraite de la moitié de l'arête du cube. Par conséquent, le ratio de dépassement s'écrit comme suit. Rmax est d'environ 21%.

Le brevet [1] du créateur du V-Cube (§20.B) spécifie un ratio optimal de 5%. Donc il est encore possible de créer un cube de dimension 2/(1-0.55*sqrt(2)) = 9.

Si le cube de dimension 11 existe, cela signifie qu'on se donne un débord de 8%. Plus R tend vers Rmax, plus N tend vers l'infini, et inversement. Il faut donc donner une limite à R sur la base de considérations physiques.

Dans la figure 11.30 du brevet illustrant la coupe transversale du V-Cube 11, on voit que les pièces se placent les unes sur les autres selon des cônes (d'où le terme de structure conique, ou inversement). Les faces se fragilisent parce que (en partant du centre) plus on va vers la couronne externe, plus les pièces sont attachées au centre du "cube". Le plastique peut alors rompre, sauf si le cube est gros, dans tel cas la résistance du matériau peut jouer contre la practabilité du jeu. C'est l'objet des remarques §19 et §22.A.

La limite physique est alors facilement donnée par la tolérance qu'on se donne sur le débord de la forme sphérique, comme calculé précédemment.

Mais alors, pourquoi les versions n°2, n°3 et n°4 n'existent pas sous la marque V-Cube ? D'après le même texte, il s'agirait paradoxalement de difficultés mécaniques (§33.B) ou de fabrication (§54 à §57) Ils existent désormais hormis le 4x4x4 (ndlr 06/2012).

Sinon, puisque le brevet ne couvre pas les dimensions supérieures à 12 (inclus), rien ne dit qu'un inventeur de génie ne trouvera pas de solution miracle.

Références : [1] EP1599261B1 (UE) et 10,555,013 (USA)

Posté par admin le 13 mai 2010 à 18:00 - Sciences
Texte soumis à la licence du site, sauf mention contraire
Rechercher plus d'informations

Commentaires

Evaluer l'article :

Ajouter un commentaire