Chemin le plus long dans un graphe orienté et cyclique

Remarque : ce document ne traite pas du chemin le plus court.

Introduction et définitions

Un graphe est tout simplement un réseau de sommets reliés entre-eux par des arcs. Une pondération peut être utilisée pour qualifier ces liens.

Des graphes ont déjà été présentés sur ce site à l'occasion du calcul de flot maximal et de la modélisation des hyperliens d'un site web.

L'algorithme de Dijkstra est connu pour rechercher le plus court chemin entre deux points connaissant le départ, l'arrivée et les routes possibles. Il peut aussi servir pour détecter rapidement s'il existe au moins un chemin entre ces deux points. Ici, dans la même situation, on veut tout le contraire : le chemin le plus long !

Qui donc a déjà su le temps qu'il faudrait pour s'aventurer vers l'inconnu ? Si Christophe Colomb en a déjà perdu le nord, nos ordinateurs vont prendre un sacré coup dans la figure.

Il faut donc émettre absolument des hypothèses simplificatrices locales pour espérer un optimum global (heuristique gloutonne), quitte à trouver UNE solution (partielle ou pas) et non LA solution. De plus, pour trouver rapidement une solution, il sera d'usage d'explorer le graphe en profondeur.

Un logiciel maison codé en C va nous aider tout au long du document. Il sait parcourir jusqu'à 1 million de noeuds par seconde.

Généralités pratiques

Pour mieux comprendre, il faut se donner des schémas explicatifs et quelques règles de base :

• Respecter le sens des flèches.
• Ne pas choisir le même point plusieurs fois lors du cheminement.

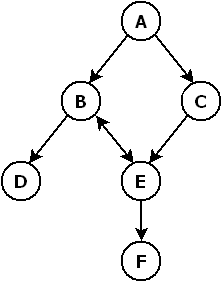
Exemple n°1

Solution : ACEBD après 12 analyses.

graph[1][0] = 2; graph[1][1] = 3;
graph[2][0] = 4; graph[2][1] = 5;
graph[3][0] = 5;
graph[5][0] = 2; graph[5][1] = 6;

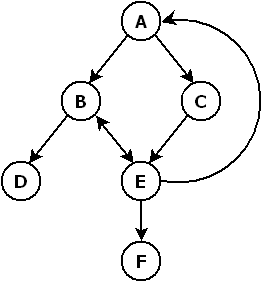
Exemple n°2

En rajoutant un arc, on change la donne :

Solutions : ACEBD et CEABD après 34 analyses.

graph[1][0] = 2; graph[1][1] = 3;
graph[2][0] = 4; graph[2][1] = 5;
graph[3][0] = 5;
graph[5][0] = 2; graph[5][1] = 6; graph[5][2] = 1;

Conclusion

En extrapolant un peu, nous déduisons :

• Le départ est idéalement une source, c'est-à-dire un cul-de-sac.
• L'arrivée peut être n'importe quel sommet (noeud ou puits) en fonction de la configuration du graphe.
• Une solution existe toujours, elle n'est pas forcément unique.
• L'ajout d'un point ou d'un arc démultiplie considérablement le nombre d'analyses.
• Selon la situation, on peut résoudre par parties.

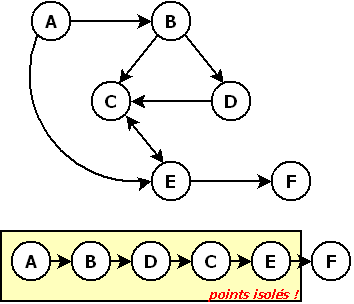
Même si ce n'est pas toujours facile, il est intéressant de pouvoir simplifier un graphe. Imaginez le gain de l'exemple suivant si F cache une monstruosité et que A est notre source :

Premier exemple

Aujourd'hui, une envie soudaine vous prend de faire un safari photo dans le métro parisien. Pour gagner du temps lors de la première expédition, vous souhaitez prendre un maximum de photos sans repasser par une station déjà photographiée.

Où commencer ? Où terminer ? Quel chemin prendre ? Quel taux d'exploration va-t-on obtenir ?

Éléments de réponse

Pour commencer, il faut récupérer le fichier des stations de métro.

On considère qu'une station est la même pour toutes les lignes qu'elle dessert. On peut donc déduire les correspondances entre les lignes.

Il existe physiquement 304 stations en rajoutant les quelques fantômes. Il faut bien voir qu'une station sans correspondance ne crée pas de calcul supplémentaire. La difficulté de l'exercice est donc mesurée par le nombre de stations permettant un changement de ligne : il y en a environ 61 !

La quasi-totalité des stations extra-muros ne paraîtront pas dans les résultats, car il sera impossible de revenir sur nos pas (cf. règle de base). Ceci dit, il faudra bien commencer par un terminus. Manifestement, la ligne 8 s'enfonce vers "Créteil-Préfecture" sans changement pendant 12 stations. Voici donc notre source idéale préférentielle.

Comme nous l'avions suggéré, aucune garantie n'est donnée quant à l'identité de la station d'arrivée.

Solution proposée

La modélisation du réseau amène au graphe suivant :

graph[1][0] = 136; graph[1][1] = 201;
graph[2][0] = 180; graph[2][1] = 234;
graph[3][0] = 198; graph[3][1] = 14;
graph[4][0] = 119; graph[4][1] = 101;
graph[5][0] = 208; graph[5][1] = 148;
graph[6][0] = 201; graph[6][1] = 16;
graph[7][0] = 235; graph[7][1] = 51;
graph[8][0] = 18; graph[8][1] = 240;
graph[9][0] = 245; graph[9][1] = 242; graph[9][2] = 247; graph[9][3] = 287;
graph[10][0] = 141;
graph[11][0] = 67; graph[11][1] = 282;
graph[12][0] = 100; graph[12][1] = 222;
graph[13][0] = 52; graph[13][1] = 133;
graph[14][0] = 3; graph[14][1] = 181;
graph[15][0] = 149;
graph[16][0] = 6; graph[16][1] = 56; graph[16][2] = 109; graph[16][3] = 129;
graph[17][0] = 260; graph[17][1] = 261;
graph[18][0] = 272; graph[18][1] = 37; graph[18][2] = 61; graph[18][3] = 140; graph[18][4] = 8; graph[18][5] = 108;
graph[19][0] = 82; graph[19][1] = 199;
graph[20][0] = 65; graph[20][1] = 113; graph[20][2] = 238; graph[20][3] = 74;
graph[21][0] = 268; graph[21][1] = 54;
graph[22][0] = 239; graph[22][1] = 108; graph[22][2] = 72; graph[22][3] = 84;
graph[23][0] = 72; graph[23][1] = 187;
graph[24][0] = 210; graph[24][1] = 167;
graph[25][0] = 192; graph[25][1] = 85;
graph[26][0] = 202; graph[26][1] = 201;
graph[27][0] = 28;
graph[28][0] = 27; graph[28][1] = 91;
graph[29][0] = 128; graph[29][1] = 291;
graph[30][0] = 123; graph[30][1] = 39;
graph[31][0] = 114; graph[31][1] = 284;
graph[32][0] = 39; graph[32][1] = 203;
graph[33][0] = 149; graph[33][1] = 98;
graph[34][0] = 35; graph[34][1] = 174;
graph[35][0] = 34;
graph[36][0] = 241; graph[36][1] = 278;
graph[37][0] = 249; graph[37][1] = 18;
graph[38][0] = 132; graph[38][1] = 219;
graph[39][0] = 30; graph[39][1] = 32;
graph[40][0] = 181; graph[40][1] = 165;
graph[41][0] = 207; graph[41][1] = 139;
graph[42][0] = 133; graph[42][1] = 280;
graph[43][0] = 269; graph[43][1] = 204;
graph[44][0] = 170; graph[44][1] = 127;
graph[45][0] = 155; graph[45][1] = 260;
graph[46][0] = 205; graph[46][1] = 142;
graph[47][0] = 133; graph[47][1] = 87;
graph[48][0] = 101; graph[48][1] = 120; graph[48][2] = 176; graph[48][3] = 67;
graph[49][0] = 175;
graph[50][0] = 145; graph[50][1] = 88;
graph[51][0] = 7; graph[51][1] = 297; graph[51][2] = 128; graph[51][3] = 288; graph[51][4] = 111;
graph[52][0] = 124; graph[52][1] = 13;
graph[53][0] = 303; graph[53][1] = 255;
graph[54][0] = 21;
graph[55][0] = 107; graph[55][1] = 284;
graph[56][0] = 166; graph[56][1] = 16;
graph[57][0] = 147; graph[57][1] = 107;
graph[58][0] = 150; graph[58][1] = 143; graph[58][2] = 212; graph[58][3] = 237; graph[58][4] = 108; graph[58][5] = 118; graph[58][6] = 211; graph[58][7] = 63;
graph[59][0] = 163;
graph[60][0] = 139; graph[60][1] = 116; graph[60][2] = 250; graph[60][3] = 188;
graph[61][0] = 275; graph[61][1] = 18;
graph[62][0] = 182; graph[62][1] = 239;
graph[63][0] = 58; graph[63][1] = 271;
graph[64][0] = 186; graph[64][1] = 170;
graph[65][0] = 123; graph[65][1] = 20;
graph[66][0] = 98; graph[66][1] = 133;
graph[67][0] = 48; graph[67][1] = 120; graph[67][2] = 152; graph[67][3] = 11; graph[67][4] = 292;
graph[68][0] = 295; graph[68][1] = 228;
graph[69][0] = 222; graph[69][1] = 78;
graph[70][0] = 228; graph[70][1] = 157;
graph[71][0] = 112; graph[71][1] = 204;
graph[72][0] = 22; graph[72][1] = 23;
graph[73][0] = 288; graph[73][1] = 177;
graph[74][0] = 20; graph[74][1] = 171;
graph[75][0] = 160; graph[75][1] = 77;
graph[76][0] = 77;
graph[77][0] = 75; graph[77][1] = 76;
graph[78][0] = 69; graph[78][1] = 251;
graph[79][0] = 252; graph[79][1] = 154;
graph[80][0] = 279; graph[80][1] = 151;
graph[81][0] = 32;
graph[82][0] = 84; graph[82][1] = 178; graph[82][2] = 172; graph[82][3] = 19;
graph[83][0] = 244; graph[83][1] = 266; graph[83][2] = 180;
graph[84][0] = 22; graph[84][1] = 82;
graph[85][0] = 25; graph[85][1] = 133;
graph[86][0] = 277; graph[86][1] = 179; graph[86][2] = 263; graph[86][3] = 293;
graph[87][0] = 47; graph[87][1] = 135;
graph[88][0] = 50; graph[88][1] = 161;
graph[89][0] = 179; graph[89][1] = 244;
graph[90][0] = 173;
graph[91][0] = 28; graph[91][1] = 117;
graph[92][0] = 131; graph[92][1] = 209;
graph[93][0] = 245; graph[93][1] = 143;
graph[94][0] = 301; graph[94][1] = 267;
graph[95][0] = 225; graph[95][1] = 174;
graph[96][0] = 140; graph[96][1] = 248;
graph[97][0] = 179; graph[97][1] = 193;
graph[98][0] = 33; graph[98][1] = 66;
graph[99][0] = 247; graph[99][1] = 275;
graph[100][0] = 130; graph[100][1] = 12;
graph[101][0] = 111; graph[101][1] = 4; graph[101][2] = 273; graph[101][3] = 48;
graph[102][0] = 153; graph[102][1] = 141;
graph[103][0] = 197; graph[103][1] = 179;
graph[104][0] = 215;
graph[105][0] = 168; graph[105][1] = 194; graph[105][2] = 215;
graph[106][0] = 240; graph[106][1] = 127; graph[106][2] = 269;
graph[107][0] = 109; graph[107][1] = 57; graph[107][2] = 207; graph[107][3] = 121; graph[107][4] = 55;
graph[108][0] = 18; graph[108][1] = 58; graph[108][2] = 22; graph[108][3] = 248;
graph[109][0] = 16; graph[109][1] = 283; graph[109][2] = 107;
graph[110][0] = 226; graph[110][1] = 155;
graph[111][0] = 51; graph[111][1] = 101;
graph[112][0] = 266; graph[112][1] = 71;
graph[113][0] = 247; graph[113][1] = 20;
graph[114][0] = 250; graph[114][1] = 31;
graph[115][0] = 132; graph[115][1] = 226;
graph[116][0] = 267; graph[116][1] = 259; graph[116][2] = 60; graph[116][3] = 188;
graph[117][0] = 91; graph[117][1] = 224;
graph[118][0] = 58; graph[118][1] = 242; graph[118][2] = 272;
graph[119][0] = 291; graph[119][1] = 4;
graph[120][0] = 135; graph[120][1] = 294; graph[120][2] = 48; graph[120][3] = 67;
graph[121][0] = 107; graph[121][1] = 247;
graph[122][0] = 173; graph[122][1] = 243;
graph[123][0] = 283; graph[123][1] = 137; graph[123][2] = 147; graph[123][3] = 30; graph[123][4] = 65;
graph[124][0] = 90; graph[124][1] = 52;
graph[125][0] = 238; graph[125][1] = 203;
graph[126][0] = 166; graph[126][1] = 136;
graph[127][0] = 285; graph[127][1] = 44; graph[127][2] = 106; graph[127][3] = 205;
graph[128][0] = 51; graph[128][1] = 29;
graph[129][0] = 16; graph[129][1] = 283;
graph[130][0] = 100;
graph[131][0] = 92;
graph[132][0] = 202; graph[132][1] = 38; graph[132][2] = 115;
graph[133][0] = 85; graph[133][1] = 66; graph[133][2] = 13; graph[133][3] = 277; graph[133][4] = 47; graph[133][5] = 42;
graph[134][0] = 243; graph[134][1] = 254;
graph[135][0] = 87; graph[135][1] = 120;
graph[136][0] = 126; graph[136][1] = 1;
graph[137][0] = 189; graph[137][1] = 123;
graph[138][0] = 159; graph[138][1] = 298;
graph[139][0] = 41; graph[139][1] = 60;
graph[140][0] = 18; graph[140][1] = 96;
graph[141][0] = 102; graph[141][1] = 10;
graph[142][0] = 46; graph[142][1] = 204;
graph[143][0] = 93; graph[143][1] = 58;
graph[144][0] = 209; graph[144][1] = 235;
graph[145][0] = 217; graph[145][1] = 50;
graph[146][0] = 267; graph[146][1] = 202;
graph[147][0] = 283; graph[147][1] = 123; graph[147][2] = 57;
graph[148][0] = 5; graph[148][1] = 216;
graph[149][0] = 15; graph[149][1] = 33;
graph[150][0] = 190; graph[150][1] = 58;
graph[151][0] = 80; graph[151][1] = 186;
graph[152][0] = 67; graph[152][1] = 267; graph[152][2] = 237; graph[152][3] = 188;
graph[153][0] = 219; graph[153][1] = 102;
graph[154][0] = 79;
graph[155][0] = 110; graph[155][1] = 45;
graph[156][0] = 230;
graph[157][0] = 70;
graph[158][0] = 200;
graph[159][0] = 289; graph[159][1] = 138; graph[159][2] = 231;
graph[160][0] = 161; graph[160][1] = 75;
graph[161][0] = 88; graph[161][1] = 160;
graph[162][0] = 163; graph[162][1] = 227;
graph[163][0] = 59; graph[163][1] = 162;
graph[164][0] = 304; graph[164][1] = 301;
graph[165][0] = 40; graph[165][1] = 223;
graph[166][0] = 281; graph[166][1] = 169; graph[166][2] = 126; graph[166][3] = 56;
graph[167][0] = 24; graph[167][1] = 225;
graph[168][0] = 195; graph[168][1] = 105;
graph[169][0] = 221; graph[169][1] = 166;
graph[170][0] = 64; graph[170][1] = 44;
graph[171][0] = 74; graph[171][1] = 195;
graph[172][0] = 82; graph[172][1] = 233;
graph[173][0] = 174; graph[173][1] = 214; graph[173][2] = 122;
graph[174][0] = 95; graph[174][1] = 49; graph[174][2] = 173;
graph[175][0] = 124;
graph[176][0] = 273; graph[176][1] = 48; graph[176][2] = 267; graph[176][3] = 259;
graph[177][0] = 73; graph[177][1] = 301;
graph[178][0] = 248; graph[178][1] = 82;
graph[179][0] = 274; graph[179][1] = 193; graph[179][2] = 184; graph[179][3] = 103; graph[179][4] = 86; graph[179][5] = 97; graph[179][6] = 89; graph[179][7] = 296;
graph[180][0] = 83; graph[180][1] = 2;
graph[181][0] = 248; graph[181][1] = 14; graph[181][2] = 199; graph[181][3] = 255; graph[181][4] = 40; graph[181][5] = 229;
graph[182][0] = 204; graph[182][1] = 62;
graph[183][0] = 264; graph[183][1] = 290;
graph[184][0] = 246; graph[184][1] = 179;
graph[185][0] = 247; graph[185][1] = 258; graph[185][2] = 249;
graph[186][0] = 271; graph[186][1] = 151; graph[186][2] = 64; graph[186][3] = 265;
graph[187][0] = 23;
graph[188][0] = 116; graph[188][1] = 60; graph[188][2] = 152; graph[188][3] = 250; graph[188][4] = 237; graph[188][5] = 241;
graph[189][0] = 224; graph[189][1] = 137;
graph[190][0] = 292; graph[190][1] = 237; graph[190][2] = 212; graph[190][3] = 150;
graph[191][0] = 247; graph[191][1] = 257;
graph[192][0] = 291; graph[192][1] = 25;
graph[193][0] = 280; graph[193][1] = 97; graph[193][2] = 302; graph[193][3] = 179;
graph[194][0] = 105; graph[194][1] = 262;
graph[195][0] = 171; graph[195][1] = 257; graph[195][2] = 168; graph[195][3] = 198;
graph[196][0] = 216; graph[196][1] = 304;
graph[197][0] = 206; graph[197][1] = 103;
graph[198][0] = 195; graph[198][1] = 3;
graph[199][0] = 19; graph[199][1] = 181;
graph[200][0] = 232; graph[200][1] = 158;
graph[201][0] = 26; graph[201][1] = 1; graph[201][2] = 264; graph[201][3] = 6;
graph[202][0] = 253; graph[202][1] = 146; graph[202][2] = 132; graph[202][3] = 26;
graph[203][0] = 125; graph[203][1] = 286; graph[203][2] = 236;
graph[204][0] = 43; graph[204][1] = 71; graph[204][2] = 142; graph[204][3] = 289; graph[204][4] = 182;
graph[205][0] = 127; graph[205][1] = 46;
graph[206][0] = 227; graph[206][1] = 197;
graph[207][0] = 107; graph[207][1] = 41;
graph[208][0] = 5;
graph[209][0] = 92; graph[209][1] = 144;
graph[210][0] = 24;
graph[211][0] = 58; graph[211][1] = 285;
graph[212][0] = 190; graph[212][1] = 58;
graph[213][0] = 297;
graph[214][0] = 34;
graph[215][0] = 105; graph[215][1] = 104;
graph[216][0] = 148; graph[216][1] = 196;
graph[217][0] = 233; graph[217][1] = 145;
graph[218][0] = 231; graph[218][1] = 232;
graph[219][0] = 38; graph[219][1] = 153;
graph[220][0] = 281;
graph[221][0] = 169;
graph[222][0] = 12; graph[222][1] = 69;
graph[223][0] = 165; graph[223][1] = 252;
graph[224][0] = 117; graph[224][1] = 189;
graph[225][0] = 167; graph[225][1] = 95;
graph[226][0] = 115; graph[226][1] = 110;
graph[227][0] = 162; graph[227][1] = 206;
graph[228][0] = 68; graph[228][1] = 70;
graph[229][0] = 181; graph[229][1] = 268;
graph[230][0] = 262; graph[230][1] = 286; graph[230][2] = 156;
graph[231][0] = 159; graph[231][1] = 218;
graph[232][0] = 218; graph[232][1] = 200;
graph[233][0] = 172; graph[233][1] = 217;
graph[234][0] = 2;
graph[235][0] = 144; graph[235][1] = 7;
graph[236][0] = 81;
graph[237][0] = 188; graph[237][1] = 152; graph[237][2] = 58; graph[237][3] = 190;
graph[238][0] = 20; graph[238][1] = 125;
graph[239][0] = 62; graph[239][1] = 22;
graph[240][0] = 8; graph[240][1] = 106;
graph[241][0] = 188; graph[241][1] = 36;
graph[242][0] = 118; graph[242][1] = 9;
graph[243][0] = 122; graph[243][1] = 134;
graph[244][0] = 296; graph[244][1] = 89; graph[244][2] = 83;
graph[245][0] = 278; graph[245][1] = 284; graph[245][2] = 93; graph[245][3] = 9;
graph[246][0] = 279; graph[246][1] = 184;
graph[247][0] = 287; graph[247][1] = 121; graph[247][2] = 270; graph[247][3] = 9; graph[247][4] = 113; graph[247][5] = 185; graph[247][6] = 99; graph[247][7] = 191;
graph[248][0] = 108; graph[248][1] = 96; graph[248][2] = 178; graph[248][3] = 181;
graph[249][0] = 185; graph[249][1] = 37;
graph[250][0] = 188; graph[250][1] = 60; graph[250][2] = 114;
graph[251][0] = 78; graph[251][1] = 283;
graph[252][0] = 223; graph[252][1] = 79;
graph[253][0] = 301; graph[253][1] = 202;
graph[254][0] = 134; graph[254][1] = 291;
graph[255][0] = 53; graph[255][1] = 181;
graph[256][0] = 282; graph[256][1] = 279;
graph[257][0] = 191; graph[257][1] = 195;
graph[258][0] = 185; graph[258][1] = 303;
graph[259][0] = 176; graph[259][1] = 116;
graph[260][0] = 45; graph[260][1] = 17;
graph[261][0] = 17;
graph[262][0] = 194; graph[262][1] = 230;
graph[263][0] = 86; graph[263][1] = 294;
graph[264][0] = 201; graph[264][1] = 183;
graph[265][0] = 186; graph[265][1] = 276;
graph[266][0] = 83; graph[266][1] = 112;
graph[267][0] = 94; graph[267][1] = 290; graph[267][2] = 176; graph[267][3] = 152; graph[267][4] = 146; graph[267][5] = 116;
graph[268][0] = 229; graph[268][1] = 21;
graph[269][0] = 106; graph[269][1] = 43;
graph[270][0] = 284; graph[270][1] = 247;
graph[271][0] = 63; graph[271][1] = 186;
graph[272][0] = 118; graph[272][1] = 18;
graph[273][0] = 101; graph[273][1] = 176;
graph[274][0] = 276; graph[274][1] = 179;
graph[275][0] = 99; graph[275][1] = 61;
graph[276][0] = 265; graph[276][1] = 274;
graph[277][0] = 133; graph[277][1] = 86;
graph[278][0] = 36; graph[278][1] = 245;
graph[279][0] = 293; graph[279][1] = 256; graph[279][2] = 246; graph[279][3] = 80;
graph[280][0] = 42; graph[280][1] = 193;
graph[281][0] = 220; graph[281][1] = 166;
graph[282][0] = 11; graph[282][1] = 256;
graph[283][0] = 129; graph[283][1] = 123; graph[283][2] = 251; graph[283][3] = 147; graph[283][4] = 109;
graph[284][0] = 55; graph[284][1] = 31; graph[284][2] = 270; graph[284][3] = 245;
graph[285][0] = 211; graph[285][1] = 127;
graph[286][0] = 203; graph[286][1] = 230;
graph[287][0] = 9; graph[287][1] = 247;
graph[288][0] = 51; graph[288][1] = 73;
graph[289][0] = 204; graph[289][1] = 159;
graph[290][0] = 183; graph[290][1] = 267;
graph[291][0] = 29; graph[291][1] = 254; graph[291][2] = 119; graph[291][3] = 192;
graph[292][0] = 67; graph[292][1] = 190;
graph[293][0] = 86; graph[293][1] = 279;
graph[294][0] = 263; graph[294][1] = 120;
graph[295][0] = 302; graph[295][1] = 68;
graph[296][0] = 179; graph[296][1] = 244;
graph[297][0] = 213; graph[297][1] = 51;
graph[298][0] = 138; graph[298][1] = 300;
graph[299][0] = 300;
graph[300][0] = 298; graph[300][1] = 299;
graph[301][0] = 177; graph[301][1] = 164; graph[301][2] = 94; graph[301][3] = 253;
graph[302][0] = 193; graph[302][1] = 295;
graph[303][0] = 258; graph[303][1] = 53;
graph[304][0] = 196; graph[304][1] = 164;

Puisqu'on peut aller et venir d'une station (sauf dans le cas des boucles des lignes 10 et 7-bis), les terminus ne sont pas détectés comme des sources. Pour forcer un départ à partir d'un terminus, il faut ajouter une station virtuelle orientée. Il faut aussi s'assurer que le programme va rechercher ce point en premier, sinon il considèrera les stations à sens unique de circulation.

graph[305][0] = 76; //Créteil-Préfecture

Le problème est trop complexe pour être résolu complètement par un ordinateur seul. Par sa modeste apparence, il rappelle étrangement le mythe du brahmane Sissa.

Malgré tout, une réponse partielle a été apportée par notre logiciel en moins d'une minute. Le taux d'exploration est de 45%, ce qui sous-entend des scores encore meilleurs.

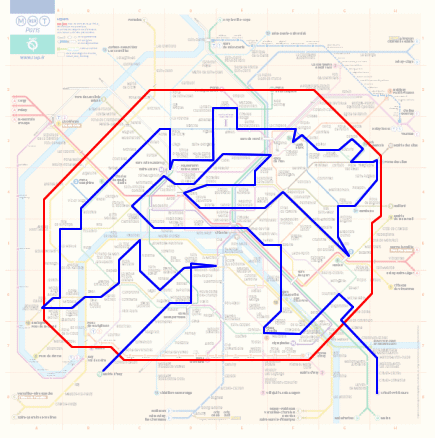
**Ligne 8**
Créteil-Préfecture
Créteil-Université
Créteil-L'Échat
Maisons-Alfort-Les Juilliottes
Maisons-Alfort-Stade
École Vétérinaire de Maisons-Alfort
Charenton-Écoles
Liberté
Porte de Charenton
Porte Dorée
Michel Bizot
Daumesnil

**Ligne 6**
Dugommier
Bercy
Quai de la Gare
Chevaleret
Nationale
Place d'Italie

**Ligne 5**
Campo-Formio
Saint-Marcel
Gare d'Austerlitz
Quai de la Rapée
Arsenal
Bastille

**Ligne 1**
Saint-Paul
Hôtel de Ville
Châtelet
Louvre-Rivoli
Palais Royal-Musée du Louvre
Tuileries
Concorde
Champs-Élysées-Clemenceau
Franklin D. Roosevelt

**Ligne 9**
Saint-Philippe du Roule
Miromesnil
Saint-Augustin
Havre-Caumartin
Chaussée d'Antin-La Fayette

**Ligne 7**
Le Peletier
Cadet
Poissonnière
Gare de l'Est

**Ligne 4**
Château d'Eau
Strasbourg-Saint-Denis

**Ligne 8**
Bonne Nouvelle
Grands Boulevards
Richelieu-Drouot
Opéra

**Ligne 3**
Quatre-Septembre
Bourse
Sentier
Réaumur-Sébastopol
Arts et Métiers
Temple
République

**Ligne 9**
Oberkampf
Saint-Ambroise
Voltaire
Charonne
Rue des Boulets
Nation

**Ligne 2**
Avron
Alexandre Dumas
Philippe Auguste
Père Lachaise

**Ligne 3**
Martin Nadaud
Gambetta

**Ligne 3-bis**
Pelleport
Saint-Fargeau
Porte des Lilas

**Ligne 11**
Télégraphe
Place des Fêtes

**Ligne 7-bis**
Pré Saint-Gervais
Danube
Botzaris
Buttes Chaumont
Bolivar
Jaurès
Louis Blanc

**Ligne 7**
Stalingrad

**Ligne 2**
La Chapelle
Barbès-Rochechouart

**Ligne 4**
Château Rouge
Marcadet-Poissonniers

**Ligne 12**
Jules Joffrin
Lamarck-Caulaincourt
Abbesses
Pigalle
Saint-Georges
Notre-Dame-de-Lorette
Trinité-d'Estienne d'Orves
Saint-Lazare

**Ligne 13**
Liège
Place de Clichy

**Ligne 2**
Rome
Villiers
Monceau
Courcelles
Ternes
Charles de Gaulle-Étoile

**Ligne 6**
Kléber
Boissière
Trocadéro

**Ligne 9**
Rue de la Pompe
La Muette
Ranelagh
Jasmin
Michel-Ange-Auteuil

**Ligne 10 (boucle validée)**
Porte d'Auteuil
Boulogne-Jean Jaurès
Michel-Ange-Molitor
Chardon Lagache
Mirabeau
Javel-André Citroën
Charles Michels
Avenue Émile Zola
La Motte-Picquet-Grenelle

**Ligne 8**
Champ de Mars
École Militaire
La Tour-Maubourg
Invalides

**Ligne 13**
Varenne
Saint-François-Xavier
Duroc

**Ligne 10**
Vaneau
Sèvres-Babylone
Croix Rouge
Mabillon
Odéon

**Ligne 4**
Saint-Germain-des-Prés
Saint-Sulpice
Saint-Placide
Montparnasse-Bienvenüe

**Ligne 12**
Falguière
Pasteur
Volontaires
Vaugirard
Convention
Porte de Versailles
Corentin Celton
Mairie d'Issy

Avec nos hypothèses, nous avons le dessin suivant qui ne peut être parcouru réellement que dans le sens Créteil->Issy :

Autres résultats

Voyons un peu l'influence du choix du point de départ :

Départ	Arrivée	Stations	Analyses
Créteil Préfecture Ligne 8	Mairie d'Issy Ligne 12	141	22 mi
Mairie d'Issy Ligne 12	Créteil Préfecture Ligne 8	140	27 mi
Mairie de Montreuil Ligne 9	Créteil-Préfecture Ligne 8	139	60 mi
Saint-Denis Université Ligne 13	Créteil-Préfecture Ligne 8	138	97 mi
La Défense Ligne 1	Saint-Denis-Université Ligne 13	132	55 mi
Olympiades Ligne 14	Mairie d'Issy Ligne 12	131	23 mi
Châtelet Ligne 1	Créteil-Préfecture Ligne 8	123	27 mi

Ces différents essais nous font toujours retomber sur Mairie-d'Issy et Créteil-Préfecture. Notre solution les réunit, donc il y a fort à parier que notre solution est bonne mais qu'il est probable qu'on puisse trouver un chemin encore plus long.

1^ère amélioration du premier exemple

Pour que notre programme chemine dans notre graphe, nous l'avons traduit à l'aide d'un tableau à deux dimensions :

• La première donne la station.
• La seconde donne les liens avec les autres stations.

Le problème

En cheminant, le programme prend les points dans l'ordre où ils lui sont présentés.

La génération du graphe a été réalisé avec un script PHP assez lent à partir d'un fichier plat énumérant les stations ligne par ligne. Du coup, c'est fatalement technique, la seconde dimension propose d'abord les antécédants dans l'ordre de parcours arbitraire de chaque ligne du plus petit numéro au plus grand, ensuite les successeurs dans l'ordre de parcours arbitraire de chaque ligne du plus grand numéro au plus petit.

Or, on a bien dit qu'il faut faire des hypothèses locales pour espérer un optimum global. On souhaite avoir un maximum de stations en peu de temps. Par conséquent, pour être en adéquation avec nos envies, on peut organiser les correspondances dans l'ordre d'importance vers une prochaine correspondance.

Alors certes, il suffirait de préparer un graphe avec comme sommets les correspondances et comme pondération le nombre de stations entre ces sommets. Sauf que le classement des correspondances suffit à se retrouver dans le même schéma. La méthode de cheminement est indépendante du graphe. De plus, le programme ne supporte pas les coefficients différents de zéro et de un.

L'optimisation

En important le fichier des stations, il n'est pas possible de trier les correspondances par ordre d'importance, car le graphe n'est pas encore intégralement construit.

L'optimisation est donc une étape supplémentaire à réaliser.

Ici, ce n'est pas une modification du graphe pour éliminer des liens inutiles. Non, c'est tout simplement une modification de sa représentation informatique pour en faciliter la reconnaissance et/ou l'exploration.

Le logiciel a deux fonctions :

• Optimiser() va à l'essentiel
• Simplifier() réduit le graphe [non implémenté]

Résultats de l'optimisation

Une fois les stations triées, voici le résultat de l'exploration sous forme d'image. Ce sera plus clair qu'une énième énumération :

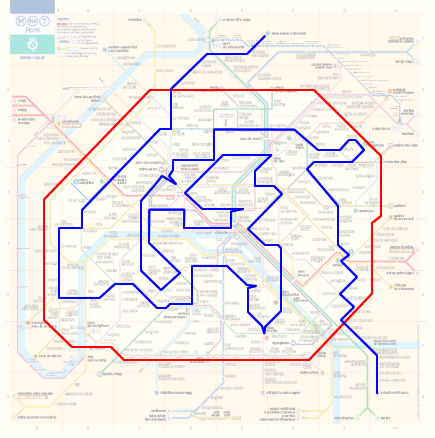
Le programme a mouliné pendant 215 millions analyses pour trouver... 134 stations seulement !

On comprend alors que l'exploration en profondeur pose problème : il faut réussir à s'en sortir quand ça commence à sentir le roussi.

2^ème amélioration du premier exemple

Le choix des premières correspondances conditionne une partie de notre résultat. Vous avez bien vu qu'en prenant à droite au lieu d'à gauche, on a trouvé une solution pire.

On peut donc se dire que si on n'a pas trouvé une bonne solution dans un délai raisonnable, on arrête une branche majeure et on passe à la suivante. Cette branche majeure peut s'étaler sur plusieurs niveaux, c'est d'ailleurs ce que nous allons choisir.

Limitation de l'exploration en profondeur

On va explorer 3 premiers niveaux de correspondance et limiter la profondeur de recherche à 30 millions chacun.

Pour cela, on modifie notre programme en lui ajoutant un compteur et les conditions qui vont bien.

Nous obtenons "Créteil-Préfecture - Saint-Denis-Université" en 139 stations. Dans le même temps que l'exemple précédent, le résultat est meilleur.

Le graphe était "trié".

3^ème amélioration du premier exemple

Le choix des correspondances est donc particulièrement surprenant : le tri réduit les résultats, le vrac initial les augmente, l'abandon les augmente.

Pour vaincre l'effet tétris, on peut implémenter une fonction Melanger() qui va mélanger les stations et ainsi forcer le programme à simuler un mouvement de type pile ou face.

Si ce choix aléatoire augmente les chemins possibles réellement explorés (effet de diversification), il n'en reste pas moins que deux lancements du même programme donneront deux résultats différents. Certes, aucun n'est plus valable que l'autre, mais avec un coup de chance, on peut probablement trouver mieux qu'auparavant.

Et c'est justement ce qu'il s'est produit avec 143 stations ! Un record qui aura été difficile à trouver.

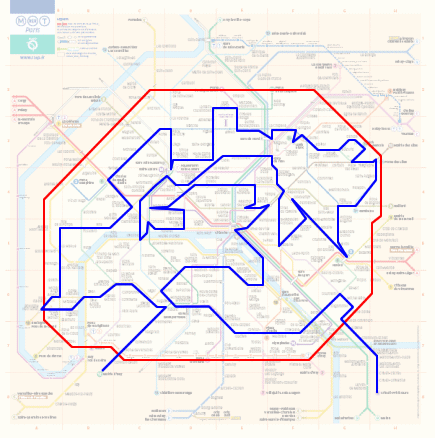
Deuxième exemple

Le travail d'un DJ est de mixer des titres les uns à la suite des autres pour donner un tout dansant où les transitions sont discrètes.

Notre unité de base sera un couple (Artiste,Titre) sans gestion des remix. Plusieurs couples forment une playlist qui dépasse rarement 15 titres. Un titre mixé n'est plus rejoué dans la même playlist.

Nous souhaitons rechercher la plus grosse playlist réalisable à partir d'une liste de playlists individuelles.

Eléments de réponse

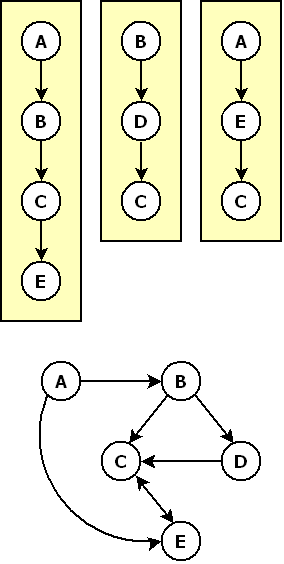
Faisons un schéma :

Le graphe du bas est un peu le graphe de mixabilité globale de la musique, dont les playlists ne sont qu'un court chemin.

En sachant quel titre peut être mixé derrière un autre, on peut former un playlist selon ses goûts. Sauf que voilà, le graphe global n'existe pas, contrairement aux playlists.

Élaboration de la solution

En ne stockant que les playlists, il faut reconstruire le graphe global.

Première étape, créer les sommets (nos couples). Une extraction distincte permet d'en dresser la liste.

Seconde étape, créer les arcs entre les chansons à partir des informations des playlists.

Troisième étape, chercher le chemin le plus long.

Vers la vérité

Notre graph est monstrueusement grand (6500 points), cyclique, orienté et idéalement pondéré... Inutile de préciser qu'on ne trouvera jamais la vraie solution attendue.

Résultat

La liste est tellement grande qu'il faut une page a elle toute seule pour l'afficher.

Le plus gros mix est ici !

Conclusion

Cette histoire de problème NP-complet est déroutante, et c'est pour cela qu'il y en a d'autres !!

À propos du programme utilisé

Même si le logiciel utilisé n'est pas disponible au téléchargement [ndlr 2023 le code source est paumé...], voici au moins ses prototypes dans l'ordre de compilation. Cela permettra à l'intéressé de structurer son programme sur la voie du succès. 335 lignes de code devraient suffir.

long __cdecl NombreAntecedants(long pNoeud);
long __cdecl DejaParcouru(long pNoeud);
void __cdecl MemoriserSolution();
void __cdecl Naviguer(long pNoeud, long pProfondeur, long pCorrespondance);
void __cdecl Initialiser();
void __cdecl Charger();
void __cdecl Simplifier();
void __cdecl Optimiser();
void __cdecl Melanger();
void __cdecl Resoudre();
void __cdecl Afficher();
void __cdecl Statistiques();
int __cdecl main(int argc, char* argv[]);

Dernière modification le 22 juillet 2018 à 19:55